Describe projectile
Any object launched into space with only gravity acting on it is referred to as a projectile. Gravity is the main force affecting a projectile. This doesn’t imply that other forces don’t affect it; it merely means that their impact is far smaller than that of gravity. A projectile’s trajectory is its route after being fired. The projectile is something like a baseball that is batted or hurled.
Projectile Motion: What Is It?
When a particle is thrown obliquely near the surface of the earth, it travels along a curved path while accelerating continuously in the direction of the planet’s center (we assume the particle stays close to the surface of the earth).
Acceleration of a particle’s projectile motion, both horizontally and vertically: When a particle is sent into the air at a certain speed, the only force acting on it is the acceleration caused by gravity (g). This downward vertical acceleration has an effect. The fact that there is no acceleration in the horizontal direction means that the particle’s horizontal velocity stays constant.
Contents
- 1 Describe projectile
- 2 Projectile Motion: What Is It?
- 3 Images of Projectile Motion Worksheet With Answers
- 4 Download Projectile Motion Worksheet With Answers
- 5 Basketball Science
- 6 Some pictures about 'Projectile Motion Worksheet With Answers'
- 6.1 projectile motion worksheet with answers pdf
- 6.2 projectile motion worksheet with answers pdf grade 9
- 6.3 projectile motion worksheet answers physics classroom
- 6.4 projectile motion word problems worksheet with answers
- 6.5 projectile motion worksheet 2 answers
- 6.6 projectile motion concepts worksheet answers
- 6.7 projectile motion comparison worksheet answers
- 6.8 mixed projectile motion worksheet answers
- 6.9 phet projectile motion worksheet answers
- 6.10 projectile motion simulation worksheet answers
- 7 Related posts of "Projectile Motion Worksheet With Answers"
Images of Projectile Motion Worksheet With Answers


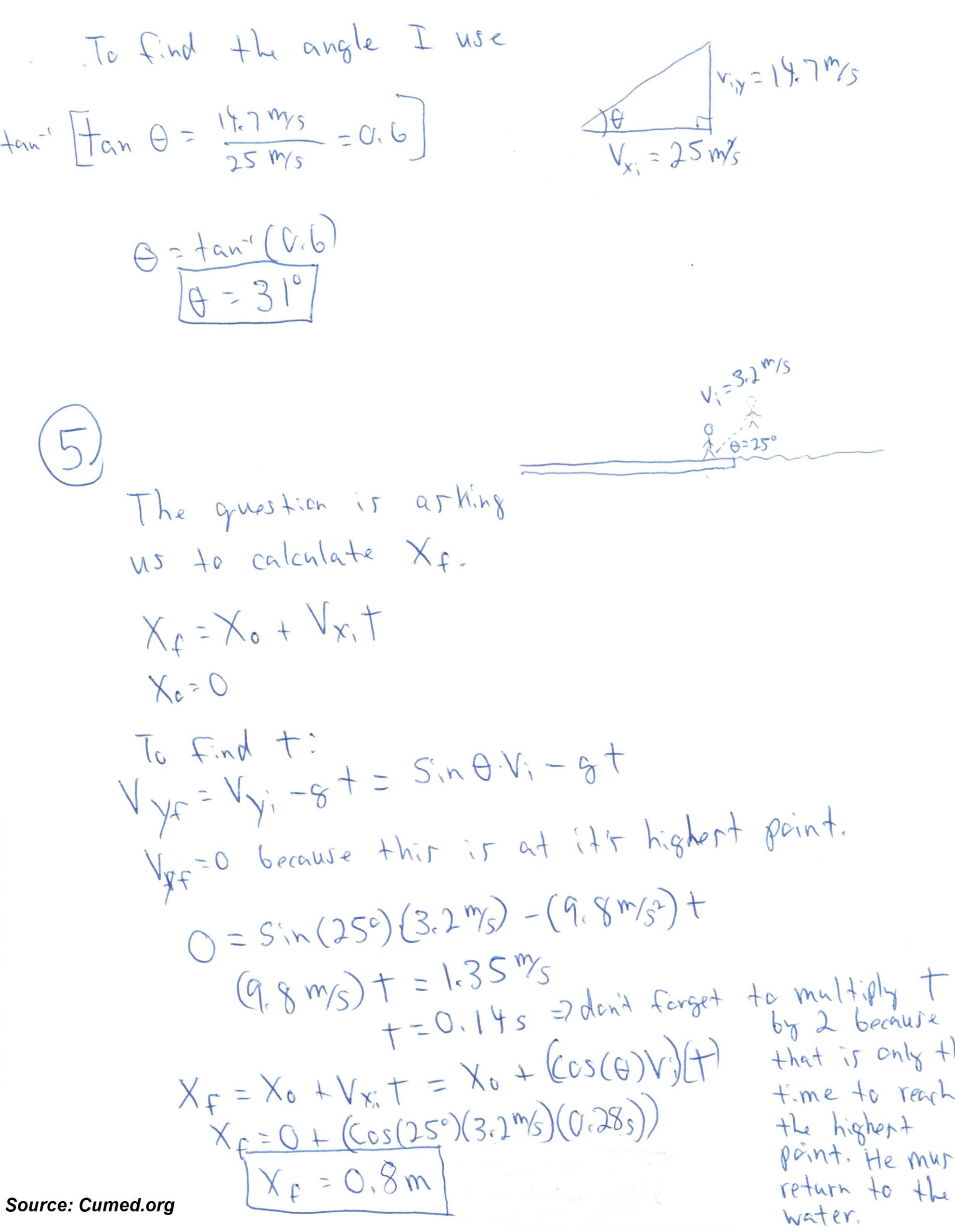

Download Projectile Motion Worksheet With Answers
Download Projectile Motion Worksheet With Answers: Click Here
Basketball Science
We are aware that two-dimensional motion, or motion on a plane, is a sort of projectile motion. It is believed that the force of gravity is the only force acting on a projectile (the thing moving as a projectile). But in the real world, how do we define projectile motion? What practical applications can be made of the principles of projectile motion? Let’s look at some actual instances of two-dimensional projectile motion.
We are all familiar with basketball. To make a basket, the player makes a small jump and tosses the ball into the hoop. The ball moves in the shape of a missile. Consequently, it is known as projectile motion. What benefit does jumping provide on their likelihood of making a basket? Aside from basketballs, all motions have one thing in common, whether it be throwing a cricket ball, a stone into a river, a javelin, an angry bird, a football, or a bullet. Each one exhibits a projectile action. And that is that gravity is the only force acting on them after they are freed. As a result, everyone of them experiences an equal and unbiased downward pull.
It indicates that if something is tossed into the air, it is simple to forecast how long it will remain in the air and how far it will travel before hitting the ground. There wouldn’t be any horizontal acceleration if the air resistance was disregarded. This suggests that a body can be thought to be moving in two dimensions, with just one direction of acceleration, as long as it is thrown close to the surface. However, how is it possible to say that a body launched into the air moves in a two-dimensional manner? Let’s assume a ball is rolling as shown below to better understand this
Now, what can we say about the dimension of motion if the ball is rolled down the path depicted? The most typical response would be that since it is travelling on a plane and has both an x-component and a y-component, it must be an instance of motion in two dimensions. However, it is incorrect because a line that can precisely define the motion of the basketball already exists. It is an illustration of one-dimensional motion as a result. As a result, the motion’s actual nature is unaffected by the axis selection.
The ball’s velocity now includes three components: an x component, a y component, and a z component if it is thrown at the angle depicted. Does this indicate that the motion is three-dimensional? Here, it is clear that a plane, not a line, can define such a motion. As a result, there is a plane that completely captures the motion of every body hurled at any angle. Thus, it can be concluded that a body will move in two dimensions no matter what projection angle is used as long as it is close to the Earth’s surface and the effects of air resistance can be ignored.
A projectile is an object that is launched into the air and then moves only in response to the acceleration of gravity. The trajectory of the object is referred to as the projectile’s path. One-Dimensional Kinematics Problem-Solving Basics describes the motion of falling objects as a straightforward one-dimensional projectile motion with no horizontal movement. This section examines the motion of two-dimensional projectiles, such as a football or other object with minimal air resistance.
The most crucial thing to keep in mind in this situation is that motions along perpendicular axes are independent and may therefore be studied separately. The independence of vertical and horizontal motions was examined in Kinematics in Two Dimensions: An Introduction. Breaking two-dimensional projectile motion into motions along the horizontal and vertical axes is the key to understanding it. Since acceleration caused by gravity is vertical, there won’t be any acceleration along the horizontal axis when air resistance is minimal (this choice of axes is the most logical). We refer to the horizontal axis as the x-axis and the vertical axis as the y-axis as is customary. The notation for displacement is shown in Figure 1, where the components of the displacement along the horizontal and vertical axes are represented by x and y, respectively, and s is defined as the overall displacement. These vectors have the magnitudes s, x, and y. (Remember that in the last section, a vector with the components Ax and Ay was denoted by the letter A. We would name displacement s with the components sx and sy if we kept the format. However, we’ll just refer to the component vectors as x and y to make the notation simpler.)
Naturally, we must deal with velocity, acceleration, and displacement when describing motion. Along the x- and y-axes, we must also locate their constituent parts. We’ll suppose that all forces, save gravity, are insignificant. Examples include friction and air resistance. Thus, the elements of acceleration are relatively straightforward: ay = -g = -9.80 m/s2. (It should be noted that this definition counts upwards as the positive direction. Gravitational acceleration assumes a positive value if the coordinate system is set up so that the downward direction is positive.) Ax = 0 since gravity is vertical. The kinematic equations can be applied because both accelerations are constant.
