Exponential Functions Worksheet Answers

The Exponential Function Explained

One of the key mathematical operations is the exponential function (though it would have to admit that the linear function ranks even higher in importance). We allow the exponent to be the independent variable to create an exponential function. The function is a straightforward instance.

The metaphor of the function machine is helpful for adding parameters to a function. The two exponential functions f(x) and g(x) above are distinct from one another, but their sole difference is a change from 2 to 1/2 in the exponentiation base. A single function machine might be used to represent both functions, but dials could also be used to show factors that affect how the machine operates.

Keep in mind that the base is now a fixed number, and the x is now in the exponent. In comparison to what we’ve seen thus far, this is quite the reverse. Up until this point, the exponent has always been a fixed value, while the base has always been a variable, often x. Despite these variations, the evaluation of these functions is precisely the same as it is for other functions. Soon, we’ll see some illustrations of exponential functions.

Business A is showing linear growth. With linear growth, the rate of change is constant, meaning that the output grows by a fixed amount for every rise in input. For firm A, the annual growth rate of new stores is constant.

Company B is unique in that our rate of change is expressed as a percentage as opposed to a fixed number of stores per year. Compare a 50% rise when there are 100 stores to a 50% increase when there are 1000 stores to see the significance of this difference:

• With 100 stores, a 50% growth would result in 50 stores that year.
• A 50% increase from 1000 stores in that year would be 500 stores.

Compound Interest Periodic

Compounding is a typical method used in finance to apply interest, whether lending or borrowing. Compounding is the process of adding one quantity on top of another before determining the final result.

We may state “my troubles are piling” linguistically. This suggests that the difficulties are not just adding up; rather, problem number 2 is complicating problem number 1 and as a result, the whole problem is more intricate than the sum of the first two problems.

When we discuss a periodic compounding interest rate, we mathematically imply that the interest earned during a given period is added to the current amount, and that the interest for the following period is then calculated based on this larger amount since it now also includes the interest earned during the previous period.

Interest rates are often represented as annual rates, or% per year, when we talk about them. Instead, if the interest is compounded over a number of annual periods, this rate is evenly divided by the number of annual periods to give us the periodic interest rate, which is then applied to the current value of the investment (or loan) for that period. Mathematically, we can determine the overall sum of.

Image of Exponential Functions Worksheet Answers

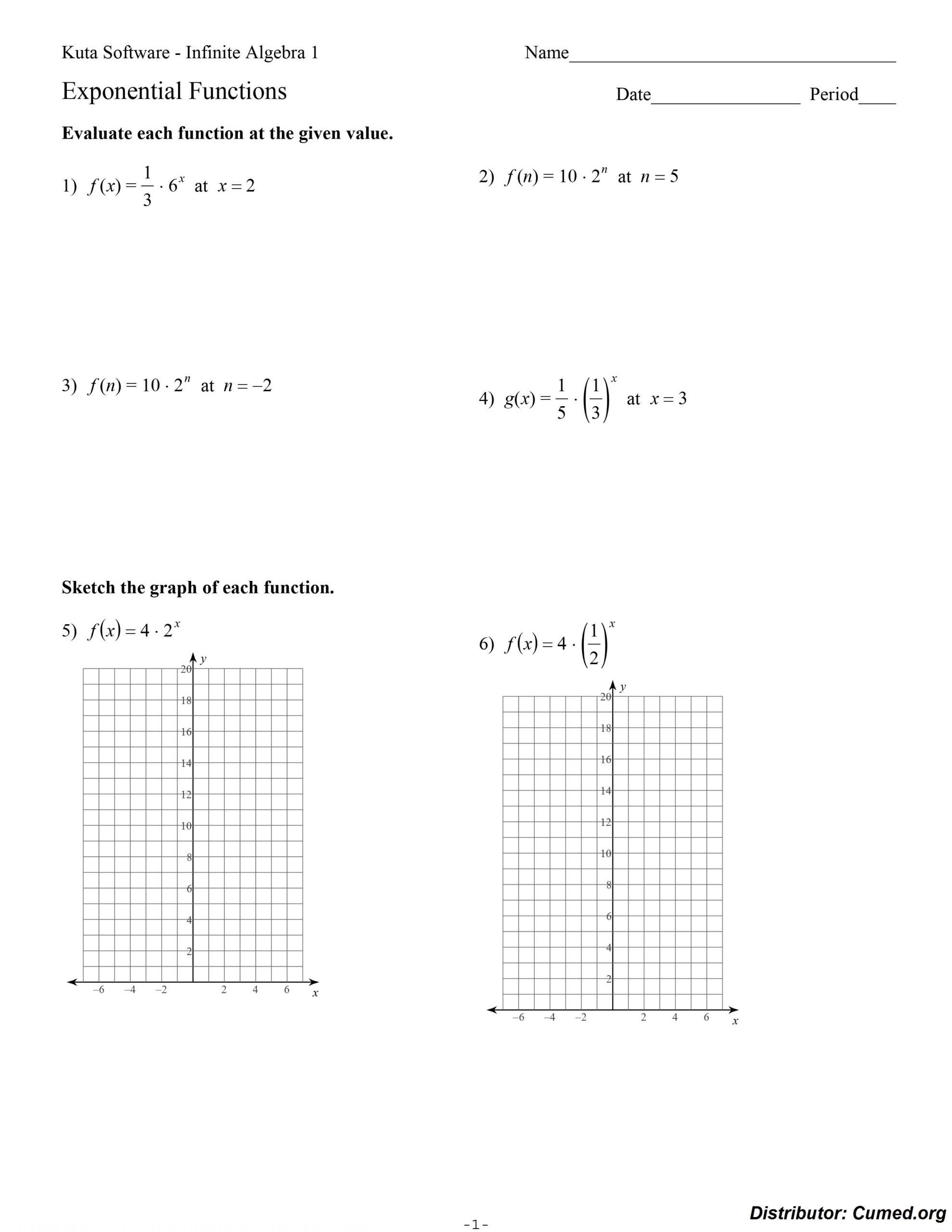
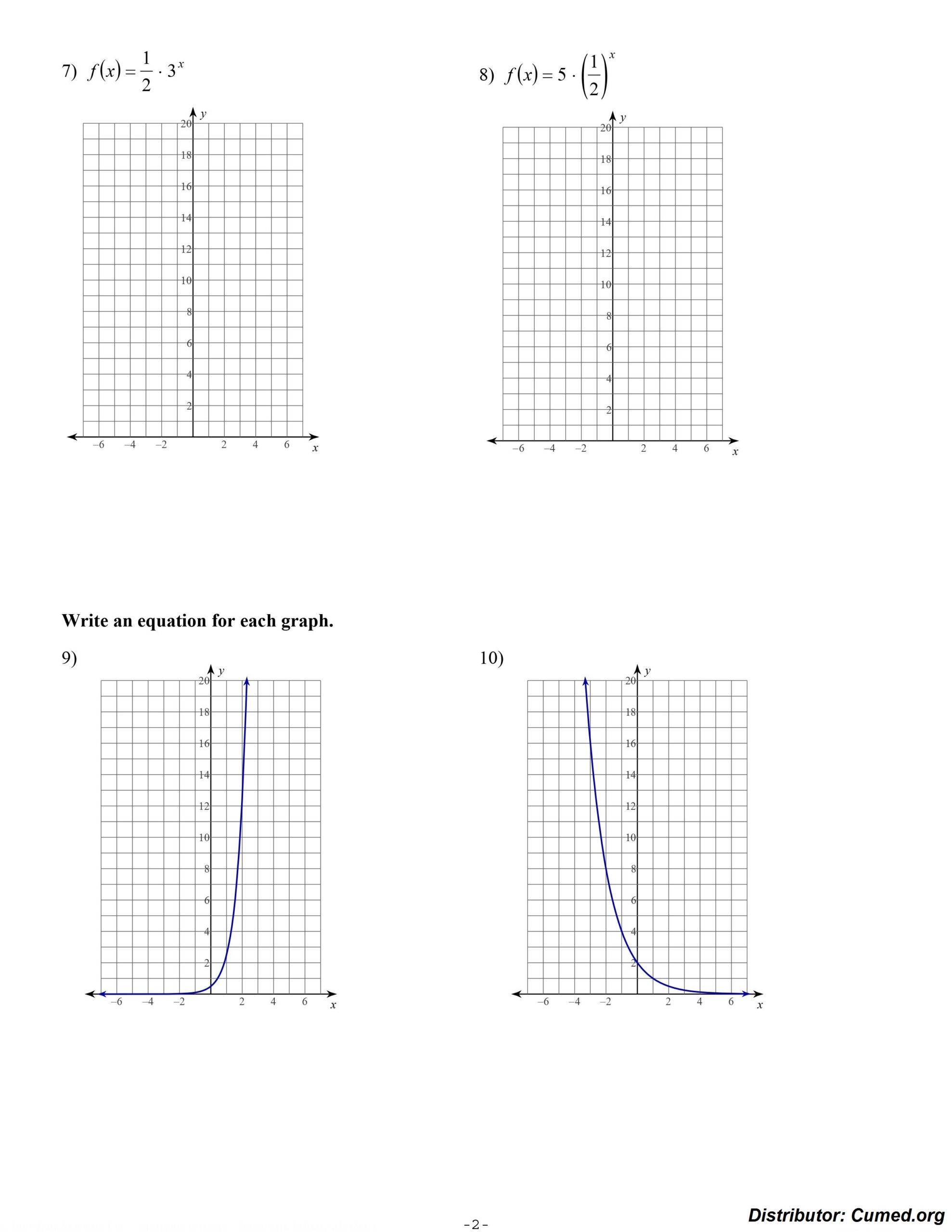
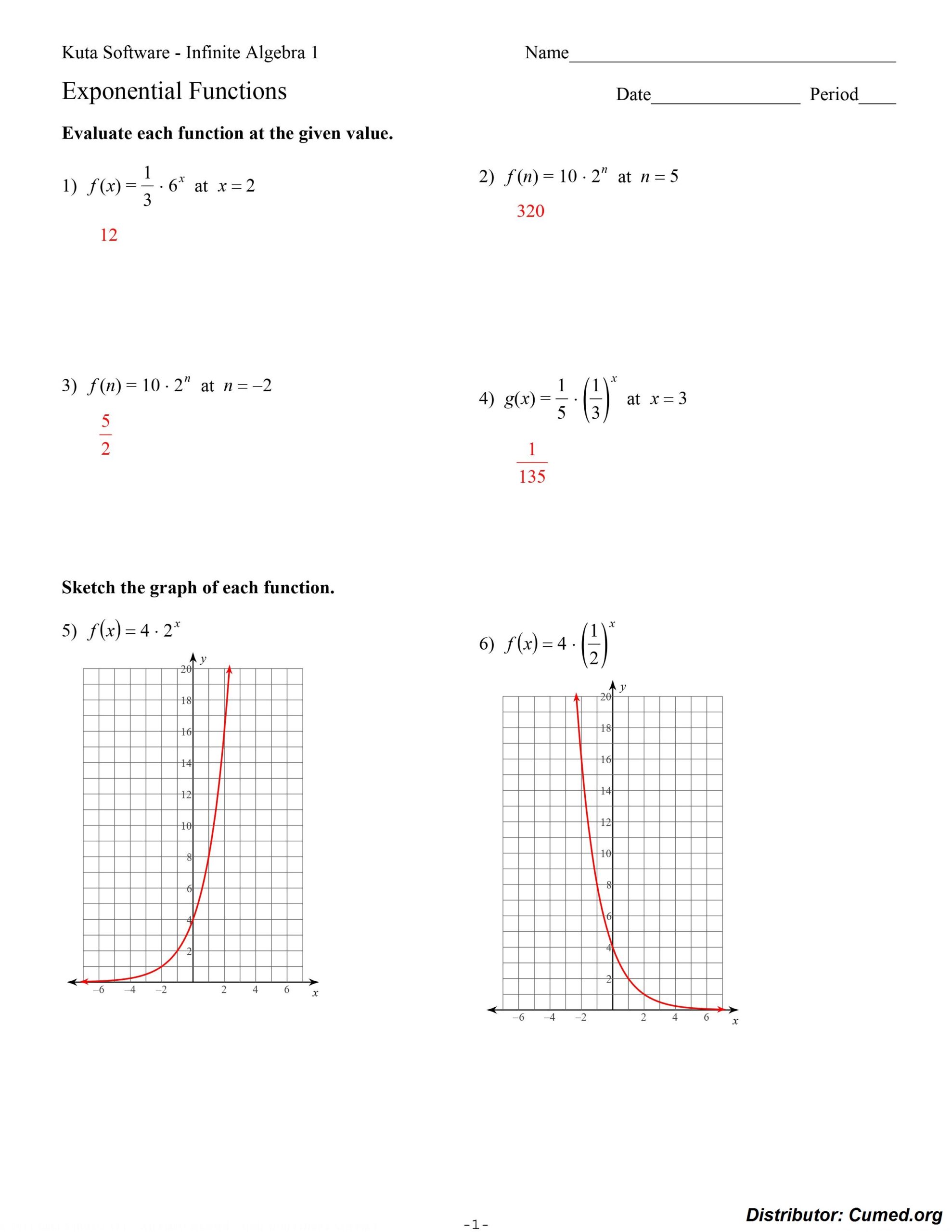
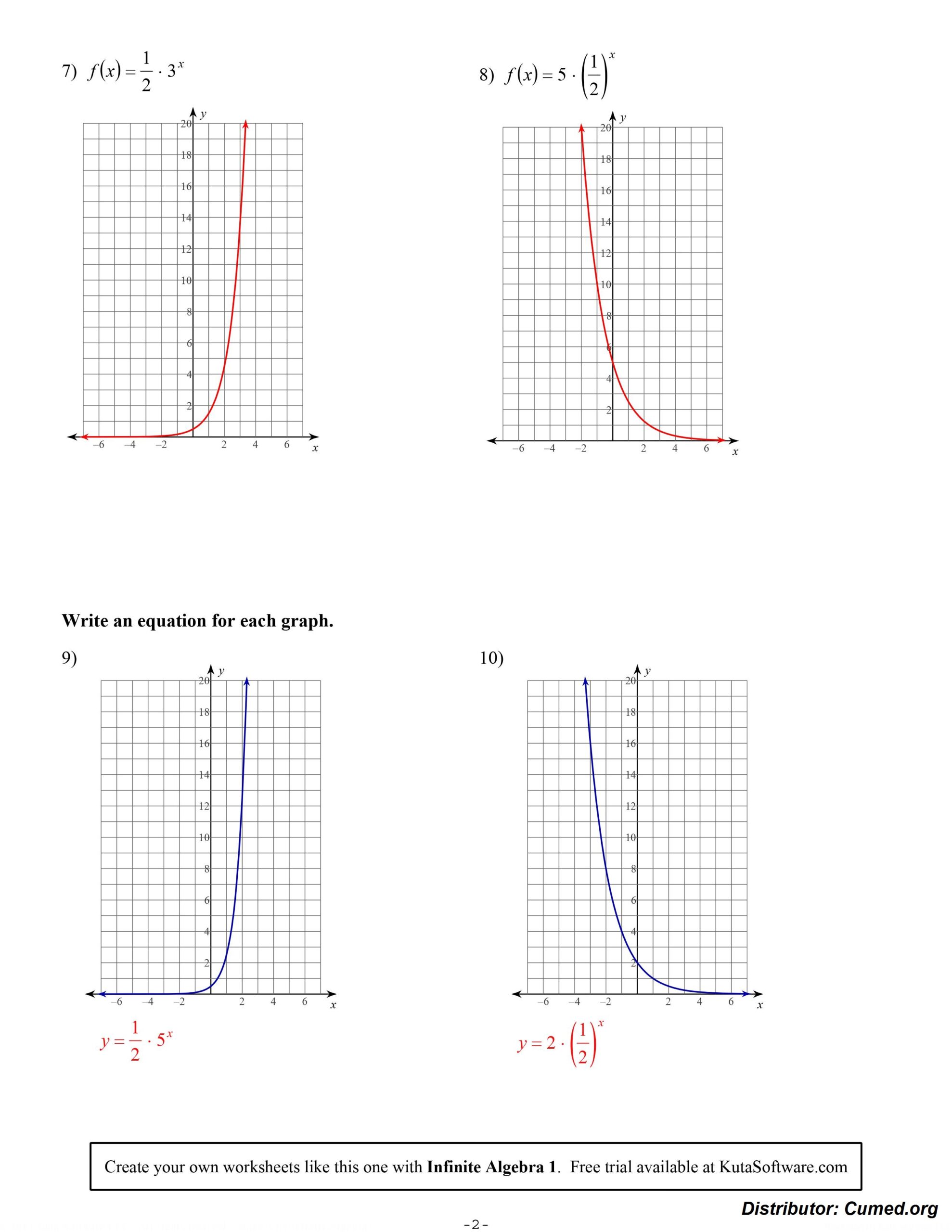
Download Exponential Functions Worksheet Answers

Download Exponential Functions Worksheet : Click Here

Download Exponential Functions Worksheet Answers: Click Here

Interest that Compounds Over Time

We must discuss a specific constant while dealing with exponentials. It comes up when we discuss things expanding continually, like continuous compounding, or continuously occurring natural occurrences, like radioactive decay. It is the number e. , sometimes known as Euler’s Number, has a specific role in characterizing a variety of mathematical occurrences. It is an irrational number, meaning it cannot be expressed as a fraction, and it has an unlimited number of non-repeating decimals, just like pi, or. According on the settings on your calculator, rounding e to an estimated value will involve using a different amount of decimals.

Some pictures about 'Exponential Functions Worksheet Answers'

Related posts of "Exponential Functions Worksheet Answers"