Pythagorean Theorem Worksheet Answers

What is the Pythagoras Theorem’s converse?

The opposite of Pythagoras’ theorem states that a triangle is a right-angled triangle if the sum of the squares of any two of its sides equals the square of its third (biggest) side.

How Does the Pythagorean Theorem Formula Work?

Only right-angled triangles can be used with the Pythagoras theorem. The Pythagoras theorem can be used to compute the unknown sides of a triangle when any two numbers are known. The Pythagoras theorem also has practical uses in the fields of engineering and architecture.

What are Some Real-World Applications of the Pythagorean Theorem?

In many different domains, the Pythagorean theorem is applied. Below are a few of its applications.

• Industries involved in architecture, construction, and navigation.
• to calculate the separation between two locations on a plane.
• for figuring out the volume, surface area, and other properties of geometric forms.

Is it possible to apply the Pythagorean Theorem Formula to any triangle?

No, because the Pythagorean theorem defines the relationship between the sides of the triangle when the square of the two legs is equal to the square of the third side, which is the hypotenuse, it can only be applied to a right-angled triangle.

The Pythagoras Theorem: Why Is It Important?

The Pythagoras theorem is significant because it facilitates the calculation of a right-angled triangle’s unknown side. Other practical uses include navigation, navigational design, and architecture and engineering.

Pythagorean Triangles

The area of the square built onto the hypotenuse of a right triangle is equal to the sum of the areas of the squares built upon the other two sides according to the Pythagorean theorem. Pythagoras squares are what these squares are called.

The Pythagoras Theorem’s uses

The Pythagoras theorem finds use in many aspects of daily life. Here are some examples of how the Pythagoras theorem is used.

Construction and engineering fields

To determine the elusive dimensions, the majority of builders employ the Pythagorean theorem technique. Calculating the diameter of a specific sector is fairly simple when length or breadth are given. In engineering applications, it is primarily employed in two dimensions.

Face detection in surveillance cameras

The Pythagorean theorem is a mathematical principle that is used by security cameras’ facial recognition functions to calculate how far a person is from the camera and how well that image will appear through the lens.

carpentry and interior design

The Pythagorean principle is used in home and building interior design and architecture.

Navigation

This method is employed by seafarers to determine the shortest path and distance between two points.

Theorem of Pythagoras

The Pythagorean Theorem, often known as Pythagoras Theorem, is a crucial concept in mathematics that describes how the sides of a right-angled triangle relate to one another. Pythagorean triples are another name for the sides of the right triangle. Here, examples help to demonstrate the formula and proof of this theorem.

In essence, the Pythagorean theorem is used to determine a triangle’s angle and length of an unknown side. This theorem allows us to obtain the hypotenuse, perpendicular, and base formulas. Let’s take a closer look at the Pythagorean theorem’s mathematics right now.

The Pythagorean Theorem

In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides, according to Pythagoras’s Theorem. These triangle’s three sides are known as the Perpendicular, Base, and Hypotenuse. Due to its position opposite the 90° angle, the hypotenuse in this case is the longest side. When the positive integer sides of a right triangle (let’s say sides a, b, and c) are squared, the result is an equation known as a Pythagorean triple.

Does the Pythagoras Theorem apply to all triangles?

No, this statement only applies to right-angled triangles.

What purpose does Pythagoras’ Theorem serve?

Theorem can be used to determine how steep mountains or slopes are. to calculate the distance between an observer and a location on the ground when the observer is looking down from a tower or building. It is mostly utilized in the construction industry.

Can the Pythagoras theorem be used to determine a square’s diagonals?

The Pythagoras theorem can be used to determine a square’s diagonals since the diagonal divides the square into right triangles.

Images of Pythagorean Theorem Worksheet Answers

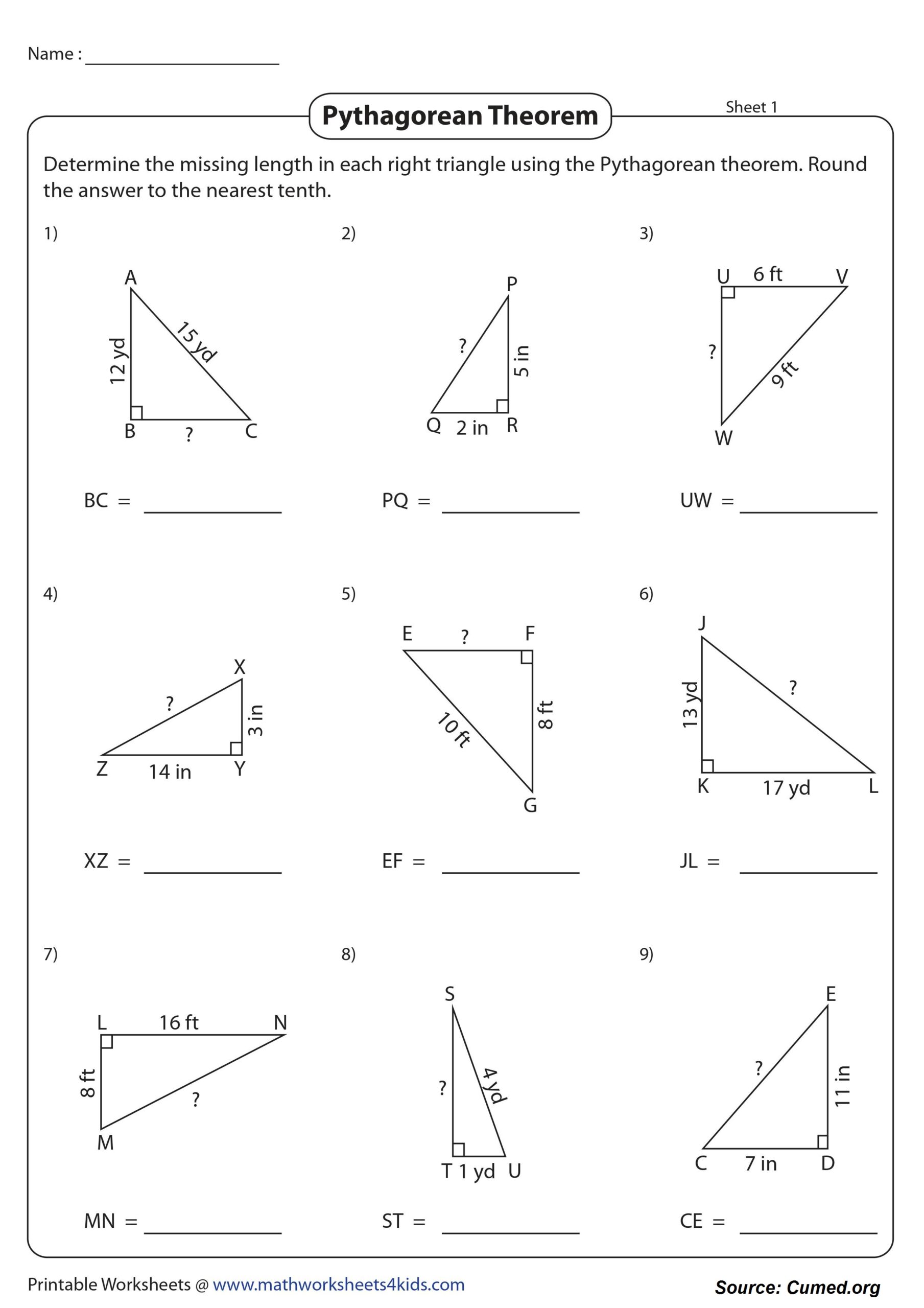
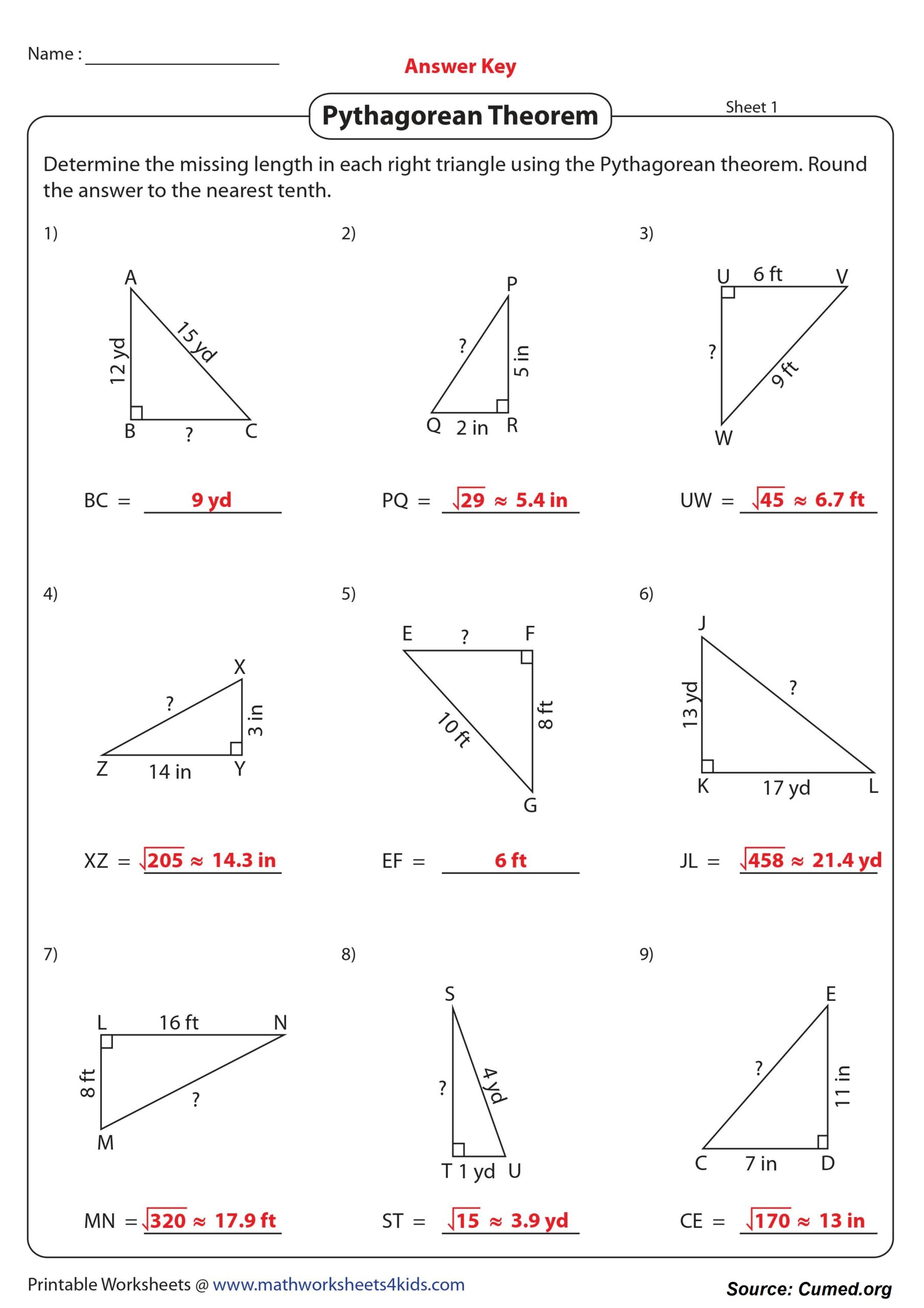
Download Pythagorean Theorem Worksheet Answers

Download Pythagorean Theorem Worksheet Answers: Click Here

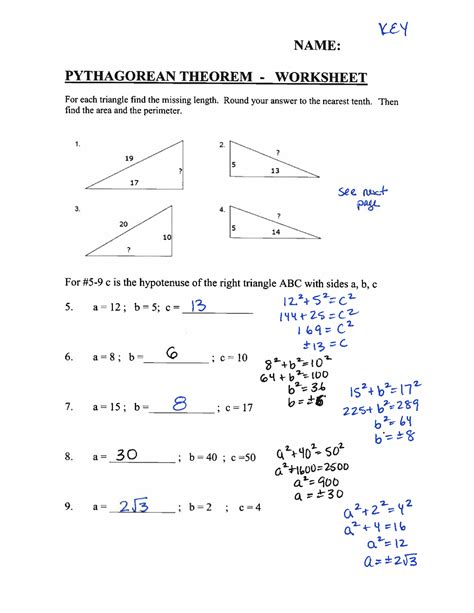
Describe how to use Pythagoras’ theorem to determine the sides of a right triangle.

• Enter the known numbers into the Pythagoras theorem formula to determine the unknown sides of a right triangle.
• simplify the equation to identify the ambiguous side.
• Find the equation’s answer for the ambiguous side.

What various methods are there for demonstrating Pythagoras’ theorem?

The Pythagoras theorem can be proven in a number of ways. Here is a list of a few of them:

• Using similar triangles as evidence
• Using differentials as evidence
• Euclid’s evidence
• mathematical proof, etc.

With Euclid’s well-known “windmill” proof of the Pythagorean theorem, Book I of the Elements comes to a close. Later in Book VI of the Elements, Euclid presents an even simpler argument utilizing the claim that the areas of comparable triangles are proportionate to the squares of their corresponding sides. (See Sidebar: Euclid’s Windmill.) He had not yet shown (as he would in Book V) that line lengths can be changed in proportions as if they were commensurable numbers, therefore it appears that Euclid contrived the windmill proof so that he could position the Pythagorean theorem as the capstone to Book I. (integers or ratios of integers). The Sidebar: Incommensurables details the issue he encountered.

There have been a plethora of original Pythagorean theorem proofs and extensions developed. Euclid himself demonstrated, using extensions as a starting point, in a theorem that was highly regarded in antiquity that any symmetrical regular figures drawn on the sides of a right triangle satisfy the Pythagorean relationship: the figure drawn on the hypotenuse has an area equal to the sum of the figures drawn on the legs. One illustration of this extension is the semicircles that make up Hippocrates of Chios’ lunes. (See Sidebar: Lune Quadrature.)

A number of problems involving determining the length of one of the sides of a right triangle when given the other two sides are presented, along with their answers, in the Nine Chapters on the Mathematical Procedures (or Nine Chapters), which were compiled in the first century CE in China. Liu Hui provided a Pythagorean theorem argument in his Commentary from the third century that involved dissecting the right triangle’s leg squares and rearranging them (“tangram style”) so that they matched the square on the hypotenuse. Even though his original drawing is lost, the following figure depicts a potential reconstruction.

There are currently more than 300 different proofs of the Pythagorean theorem, including ones by the Greek mathematician Pappus of Alexandria (who flourished around 320 CE), the Arab mathematician-physician Thbit ibn Qurrah (who lived from 836 to 901), the Italian artist-inventor Leonardo da Vinci (who lived from 1452 to 1519), and even American President James Garfield (1831–81).

Related posts of "Pythagorean Theorem Worksheet Answers"