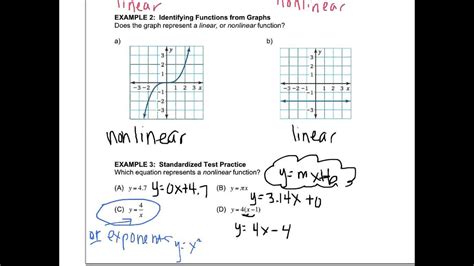
The Linear and Nonlinear Functions Worksheet can be a great resource for students to explore the differences between linear and nonlinear functions. It can help students understand the relationships between different types of equations and how they are used to represent data in different ways. The worksheet helps students practice graphing and using linear and nonlinear equations to solve real-world problems. It also introduces students to the concept of nonlinear functions and how they can be used to model complex relationships. This worksheet can help students develop a better understanding of linear and nonlinear functions and how they can be used to represent and analyze data.
Analyzing Linear and Nonlinear Functions: A Step-by-Step Guide
Welcome to this step-by-step guide to analyzing linear and nonlinear functions. In this guide, we will cover the basics of linear and nonlinear functions, how to identify and distinguish between them, and how to analyze them. We will also discuss the importance of understanding these functions and the various applications they have in mathematics and other fields.
Linear functions are equations that can be expressed in the form of y=mx+b, where m and b are constants. These equations produce a straight line when graphed, and the slope of the line is equal to m. Linear functions are some of the most basic functions used in mathematics, and they have many practical applications.
Contents
- 0.1 Analyzing Linear and Nonlinear Functions: A Step-by-Step Guide
- 0.2 How to Graph Linear and Nonlinear Functions on a Worksheet
- 0.3 Understanding the Relationship between Linear and Nonlinear Functions
- 0.4 Exploring the Differences between Linear and Nonlinear Functions
- 0.5 Utilizing the Linear and Nonlinear Functions Worksheet to Strengthen Mathematical Concepts
- 0.6 Images of Linear And Nonlinear Functions Worksheet Answer Key
- 0.7 Download Linear And Nonlinear Functions Worksheet Answer Key
- 1 Conclusion
Nonlinear functions, on the other hand, are equations that cannot be expressed as y=mx+b. These equations produce curves when graphed, and they may have multiple slopes. Nonlinear functions are more complex than linear functions, and they are used in more advanced mathematical applications.
To identify a linear or nonlinear function, you must first look at the equation and determine whether it can be expressed as y=mx+b. If the equation can be expressed in this form, it is a linear function. If the equation cannot be expressed in this form, it is a nonlinear function.
Once you have identified the type of function, you can analyze it. For linear functions, you can use the slope-intercept form of the equation to determine the slope and intercept of the line. You can then use this information to analyze the function further, such as determining its rate of change and intercept.
For nonlinear functions, you can use various methods to analyze the function. You can use calculus to determine the derivatives of the function and their properties. You can also use graphical methods to analyze the behavior of the function by graphing it and looking for patterns.
It is important to understand linear and nonlinear functions, as they are used in a variety of applications. Linear functions are used in economics to describe consumer demand, while nonlinear functions are used in physics to describe the behavior of particles. Understanding these functions is essential for many fields of study, and having a good grasp of them can help you succeed in your studies.
We hope this step-by-step guide has provided you with a better understanding of linear and nonlinear functions. If you are still unsure, you can consult your instructor or a mathematics textbook for more guidance. Good luck!
How to Graph Linear and Nonlinear Functions on a Worksheet
Graphing linear and nonlinear functions on a worksheet can be an important tool for understanding and interpreting these functions. In order to graph linear and nonlinear functions on a worksheet, there are a few steps that must be taken.
First, it is necessary to determine which type of function is being graphed. A linear function is a function whose graph is a straight line. A nonlinear function, on the other hand, is a function whose graph is curved. Once the type of function has been identified, the next step is to plot the points that define the function on the worksheet.
For a linear function, the points should be plotted on the worksheet in two dimensions, with the x-axis representing the independent variable and the y-axis representing the dependent variable. For a nonlinear function, the points should be plotted on the worksheet in three dimensions, with the x-axis representing the independent variable, the y-axis representing the dependent variable, and the z-axis representing the third dimension.
Once the points have been plotted, a line or curve can be drawn that connects the points. For a linear function, the line should be a straight line. For a nonlinear function, the curve should be a smooth curve that does not cross itself.
Finally, it is important to label the axes and the line or curve to make it easier to interpret the function. Labeling the axes should include the type of function being graphed and the range of values for each axis. For the line or curve, the equation of the function should be included.
By following these steps, it is possible to accurately graph linear and nonlinear functions on a worksheet. This can be a useful tool for interpreting and understanding these functions and their relationships.
Understanding the Relationship between Linear and Nonlinear Functions
Linear and nonlinear functions are two distinct types of functions that are used to describe mathematical relationships between two or more variables. Linear functions are those that have a constant rate of change, meaning that a change in one variable results in a consistent change in the other variable. In contrast, nonlinear functions have a variable rate of change, meaning that a change in one variable does not necessarily result in a consistent change in the other variable.
Linear functions are often represented by straight lines on a graph, while nonlinear functions are represented by curves. Linear functions can be expressed as an equation in the form of y = mx + b, where m is the slope of the line and b is the y-intercept. Nonlinear functions, on the other hand, cannot be expressed in such a simple equation.
The key difference between linear and nonlinear functions is that linear functions have a constant rate of change, while nonlinear functions have a variable rate of change. Linear functions tend to be easier to work with because they can be expressed in a single equation, while nonlinear functions are more complicated and often require more advanced mathematical techniques.
Linear and nonlinear functions are both used to describe relationships between two or more variables. Linear functions are often used to describe relationships between two variables, while nonlinear functions are often used to describe relationships between three or more variables. In any case, it is important to understand the difference between linear and nonlinear functions in order to properly interpret mathematical relationships.
Exploring the Differences between Linear and Nonlinear Functions
Linear and nonlinear functions are two different types of mathematical equations used to represent relationships between variables. They have distinct characteristics that differentiate them from each other and are used in a variety of contexts. This article will explore the differences between the two and discuss their uses.
Linear functions are equations that have a constant rate of change between the two variables. This means that if x increases by one unit, then y will also increase by a constant amount. Linear functions are represented by straight lines on a graph and can be described using the equation y = mx + b, where m is the slope and b is the y-intercept.
Nonlinear functions, on the other hand, have a rate of change that is not constant. This means that if x increases by one unit, then y may not increase by a constant amount. Nonlinear functions are represented by curved lines on a graph and can be described using equations such as polynomials, exponentials, and logarithms.
Linear functions are used to model many real-world situations where the rate of change between two variables remains constant. For example, in economics, linear functions are used to describe the relationship between the price of a good and its demand.
Nonlinear functions are used to model situations where the rate of change between two variables is not constant. For example, in physics, nonlinear functions are used to describe the motion of an object under the influence of gravity.
In conclusion, linear and nonlinear functions are two different types of mathematical equations used to represent relationships between variables. They have distinct characteristics that differentiate them from each other and are used in a variety of contexts. Linear functions are used to model situations where the rate of change between two variables remains constant, while nonlinear functions are used to model situations where the rate of change between two variables is not constant.
Utilizing the Linear and Nonlinear Functions Worksheet to Strengthen Mathematical Concepts
Mathematical concepts are an integral part of our lives and understanding them is critical to our success in many areas. The Linear and Nonlinear Functions Worksheet is a great tool to help strengthen mathematical concepts. This worksheet can be used as an individual practice activity, or as a group activity.
The Linear and Nonlinear Functions Worksheet begins with an introduction to linear and nonlinear functions. It provides several examples of linear and nonlinear functions and explains how to identify them. The worksheet then provides a set of practice problems that students can work through to test their understanding of the concepts. The worksheet also provides an answer key for the practice problems.
The Linear and Nonlinear Functions Worksheet has several advantages. First, it provides a clear explanation of the concepts, making it easier for students to understand. Second, it provides practice problems that can be used to test the student’s understanding of the concepts. Third, it provides an answer key that can be used to check the student’s solutions.
This worksheet is an excellent tool to help students strengthen their understanding of linear and nonlinear functions. The worksheet can be used to help reinforce the concepts discussed in class, as well as to help students check their understanding of the concepts. Furthermore, the worksheet can be used to help students develop problem solving skills.
The Linear and Nonlinear Functions Worksheet is an excellent way to help students strengthen their understanding of mathematical concepts. This worksheet can be used as an individual practice activity, or as a group activity to help students better understand the concepts. The worksheet provides a clear explanation of the concepts, practice problems, and an answer key to help students check their solutions. By using the Linear and Nonlinear Functions Worksheet, students can strengthen their understanding of mathematical concepts and develop problem solving skills.
Images of Linear And Nonlinear Functions Worksheet Answer Key


Download Linear And Nonlinear Functions Worksheet Answer Key
Download Linear And Nonlinear Functions Worksheet Answer Key: click here
Conclusion
This worksheet provided a great introduction to linear and nonlinear functions and their graphs. It emphasized the importance of understanding the concept of slope, and how linear and nonlinear equations and graphs can be used to solve problems. It also provided a great opportunity for students to practice graphing and interpreting linear and nonlinear functions. By completing this worksheet, students should have a better understanding of linear and nonlinear functions and be better prepared to work with them in the future.