Graphing Proportional Relationships Worksheet

What is a Proportional Relationship on a Graph?

• The amount of money we must spend and the number of gallons of fuel we add to our car’s fuel tank at the gas station are proportionate.
• If we pay $10 for a bag of chips, we will pay $20 for two bags and $30 for three bags. The amount of money we spend and the number of bags of chips we purchase are proportionate.
• If a person is paid $100 for working one hour, he will be paid $200 for working two hours, and $300 for working three hours. The amount of money he is paid is directly proportionate to the number of hours he works.
• In the event that someone is trying to lose weight and does so by losing 1 kg in 10 days, 2 kg in 20 days, and 3 kg in 30 days. The weight he is losing and the number of days it takes him to lose it are inversely proportional. The amount of weight he loses over the upcoming months will depend in part on this relationship.

Ordered data pairs graphed

You will learn how to plot ordered pairs of points that represent data from a proportional relationship in this part.

The relationship between the two variables in a piece of data can be seen by graphing ordered pairs on a coordinate plane.

Think about the following circumstance as you practice graphing ordered pairs of data.

Melanie is a messenger. She drew a chart of the routes she took that day, noting the time it took her to complete each mile.

Proportional relationships can be graphed.

Under the 8th grade (U.S.) Math Mission, there is an exercise called “Graphing proportional relationships.” This activity highlights the linearity and growth through the origin of proportional relationships.

types of issues

In this activity, there are three different kinds of problems:

• Graph and describe the data: In this exercise, students are given a proportional connection to graph and are asked to choose the proper summaries from a multiple-choice list.
• The student is given a proportional relationship in this problem, and they are asked to graph it and determine the relationship’s equation.
• The student is given a proportional connection in this issue, and they are asked to graph it and determine the unit change, which is equivalent to the slope.

PROPORTIONAL RELATIONSHIPS: WHAT ARE THEY?

If every pair of data values is related in the same way, by multiplying by a factor, then the relationship is proportional. A proportionate relationship can be identified by looking at data, an equation, or a graph.

Use a proportionate connection to make muffins.

Two eggs are required to make one dozen muffins. 4 eggs are required to make 2 dozen muffins. There are 6 eggs required to create 3 dozen muffins. 1 plus 2 equals 2, 2 plus 2 equals 4, 3 plus 2 equals 6. Every time, there are two times as many batches of muffins as eggs. A proportionate relationship is what we have here.

What is a relationship that is directly proportional?

A relationship is said to be directly proportional if two quantities are connected in such a way that an increase in one quantity causes a comparable rise in the other and vice versa. We refer to two quantities as being proportionate to one another if their relationship is direct. Let’s look at an illustration. Let’s think about the quantity of items a person purchased and the total cost. It is obvious that the sum paid will increase as the quantity of articles increases. As a result, the quantity of goods purchased and the price paid are directly proportionate to one another.

Proportional Relationships Graphing

With the help of this math worksheet for eighth grade, practice graphing proportional relationships and determining the constant of proportionality. Students are given multiple word problems in this two-page worksheet that each have a ratio that describes a proportionate relationship between two quantities. Students will calculate the proportionality constant from the above ratios and then plot a graph for each proportional relationship. This activity is a fantastic approach for students to practice identifying and graphing proportional connections while also learning how the ideas are used in practical situations. For additional focused practice, look at Graph Proportional Relationships #1 and Graph Proportional Relationships #2!

Graph proportional relationships, supposing the slope of the graph to be the unit rate. Compare the two distinct proportional relationships that are illustrated in various ways. Consider comparing a distance-time graph with an equation for distance-time to determine which of two moving objects is moving at a faster rate.

Graph proportional relationships, supposing the slope of the graph to be the unit rate. Compare the two distinct proportional relationships that are illustrated in various ways.

Recognize the links between lines, linear equations, and proportional relationships.

Graph proportional relationships, supposing the slope of the graph to be the unit rate. Compare the two distinct proportional relationships that are illustrated in various ways. Consider comparing a distance-time graph with an equation for distance-time to determine which of two moving objects is moving at a faster rate.

Worksheets for Graphing Proportional Relationships

How are proportional relationships graphed? Let’s say your teacher requests you to plot a proportional relationship (x and y) with a unit rate of 0.4, meaning that changing x by one unit will result in changing y by 0.4 units. Consider some possible values between x and y. Keep in mind that x and y are independent values in this situation. That implies that a certain value of y will be equivalent to a constant multiplied by x. If we were to use an expression to represent this, it would look like this: X, Y = (0, 0), (1, 0.4), (2, 0.8), (3, 1.2), (4, 1.6), where K equals any constant number (5, 2) You would know that a straight line would be drawn if you tried to graph these values. It demonstrates the proportional relationship in the graph. Students will learn how to graph and recognize graphs of proportional relationships through this set of courses and activities.

Images of Graphing Proportional Relationships Worksheet

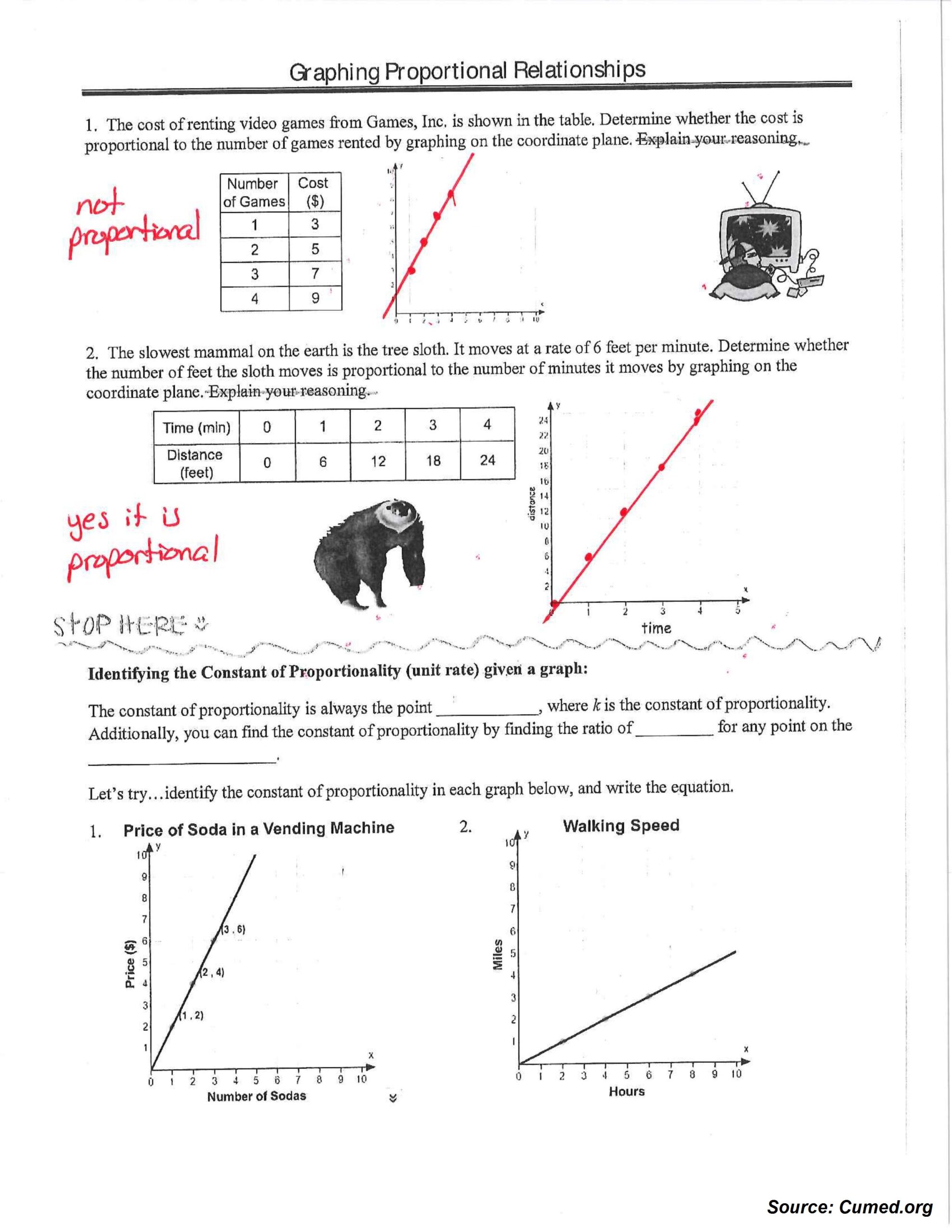
Free Download Graphing Proportional Relationships Worksheet

Free Download Graphing Proportional Relationships Worksheet: Click Here

Understanding Proportional Relationships in Graphs

A proportional relationship between two variables means that they always exist in the same ratio to one another. This indicates that they will initially form a line that passes through the origin when they are shown on a line graph (0, 0). They will be a part of the equation y = kx in some way. For you, this means that as x rises, y follows. The x value will decrease if the y value does. They are therefore in constant proportion to one another. These variables will always be relative to one another, no matter how large or little their values are.

Some pictures about 'Graphing Proportional Relationships Worksheet'

Related posts of "Graphing Proportional Relationships Worksheet"